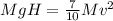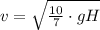Question

A uniform solid ball with a mass , M, is placed at the top of an inclined plane and released. What will be the velocity of the ball at the bottom of the incline? The vertical height of the incline from which the ball was released is H.

Answer 1

Answer:
`v=\sqrt{(10)/(7)\cdot gH}`

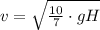
Step-by-step explanation:

Given

Mass of ball is M

Height of incline is H

Here conservation of energy will provide the velocity at bottom

Energy at top of incline plane
`=MgH`

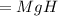
Energy at bottom=Kinetic energy+Rotational energy

Assuming Pure rolling we can write

`v=\omega R`

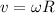
where
`v`=velocity of ball

`\omega`=angular velocity of ball

R=radius of ball

`E_b=(1)/(2)Mv^2+(1)/(2)I\omega ^2`

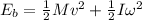
where I=moment of inertia of ball

`I=(2)/(5)MR^2`

`E_b=(1)/(2)Mv^2+(1)/(2)* (2)/(5)MR^2* ((V)/(R))^2`

`E_b=(7)/(10)Mv^2`

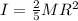
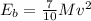
Now ,

`MgH=(7)/(10)Mv^2`

`v=\sqrt{(10)/(7)\cdot gH}`