Answer:
Because the actual identity says
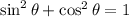
Explanation:
The trigonometric ratios
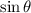 and
and
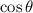 have a maximum value of 1. And hence
have a maximum value of 1. And hence
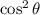 and
and
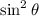 will have values between 0 and 1 as they are squares and will be always positive.
will have values between 0 and 1 as they are squares and will be always positive.
But if we look at the equation
 shows that
shows that
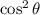 will be more than 1. Hence it is an incorrect equation.
will be more than 1. Hence it is an incorrect equation.
The correct relation between
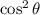 and
and
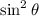 is
is
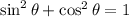 .
.