Question

A certain Bookstore that sells A Million books wants to hire you, and you get the job if you can answer these problems correctly. Suppose that the number of books that the store sells each minute has a Poisson distribution with a known rate of 1.3 books per minute. a) What's the probability that the store will sell 2 books in the next minute? b) What's the probability that the store will sell less than 4 books in the next minute? c) What's the probability that the store will sell at least 3 books in the next minute given that it sells at least 2 books in the next minute?

Answer 1

a) P ( X = 2 ) = 0.23028

b) P ( X < 4 ) = 0.95689

c) P ( X ≥ 3 | X ≥ 2 ) = 0.38292

Explanation:

Given:-

- The parameter for the poisson distribution is given, λ = 1.3.

- Declare a random variable (X) which is the number of books sold in the next minute:

X ~ Po (1.3)

Find:-

a) What's the probability that the store will sell 2 books in the next minute? b) What's the probability that the store will sell less than 4 books in the next minute? c) What's the probability that the store will sell at least 3 books in the next minute given that it sells at least 2 books in the next minute?

Solution:-

a) The required probability P ( X = 2 ). Can be computed by using the pmf for the poisson distribution:

`P(X = x ) =( (lambda)^k e^(^-^l^a^m^b^d^a^))/(k!)\\\\P(X = x ) =( (1.3)^k e^(^-^1^.^3^))/(k!)`

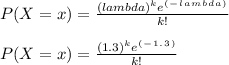
Where, "k" is the number of books sold in next minute.

- Now compute P ( X = 2 ) :

`P(X = 2 ) =( (1.3)^2 e^(^-^1^.^3^))/(2!)\\\\P(X = 2 ) = 0.23028`

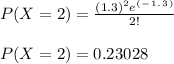
b) The required probability P ( X < 4 ). Can be computed by using the pmf for the poisson distribution and summing individual terms from 0 - 3:

`P(X < 4 ) = P ( X = 0) + P ( X = 1 ) + P ( X = 2 ) + P ( X = 3 )\\\\P(X < 4 ) = ( (1.3)^0 e^(^-^1^.^3^))/(0!)+ ( (1.3)^1 e^(^-^1^.^3^))/(1!)+ ( (1.3)^2 e^(^-^1^.^3^))/(2!) + ( (1.3)^3 e^(^-^1^.^3^))/(3!)\\\\P(X < 4 ) = 0.27253 + 0.35429 + 0.23028 + 0.09979 = 0.95689`

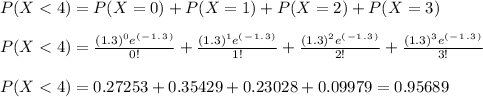
c) The required probability P ( X ≥ 3 | X ≥ 2 ). We have to consider the conditional probability as follows:

P ( X ≥ 3 | X ≥ 2 ) = P ( X ≥ 3 & X ≥ 2 ) / P (X ≥ 2 )

= P ( X ≥ 3 ) / P (X ≥ 2 )

= P ( X > 2 ) / P ( X > 1 )

= [ 1 - P ( X ≤ 2 ) ] / [ 1 - P ( X ≤ 1 ) ]

- Compute P ( X ≤ 2 ) & P ( X ≤ 1 ) using pmf:

P ( X ≤ 2 ) = 0.27253 + 0.35429 + 0.23028

= 0.8571

P ( X ≤ 1 ) = 0.27253 + 0.35429

= 0.62682

- Use the expression developed for conditional probability to evaluate the required probability:

P ( X ≥ 3 | X ≥ 2 ) = [ 1 - P ( X ≤ 2 ) ] / [ 1 - P ( X ≤ 1 ) ]

= [ 1 - 0.8571 ] / [ 1 - 0.62682 ]

= 0.38292