Question

Suppose a simple random sample of size nequals81 is obtained from a population with mu equals 79 and sigma equals 18. ​(a) Describe the sampling distribution of x overbar. ​(b) What is Upper P (x overbar greater than 81.2 )​? ​(c) What is Upper P (x overbar less than or equals 74.4 )​? ​(d) What is Upper P (77.6 less than x overbar less than 83.2 )​?

Answer 1

(a) The sampling distribution of
`\overline{X}` = Population mean = 79

(b) P (
`\overline{X}` greater than 81.2 ) = 0.1357

(c) P (
`\overline{X}` less than or equals 74.4 ) = .0107

(d) P (77.6 less than
`\overline{X}` less than 83.2 ) = .7401

Explanation:

Given -

Sample size ( n ) = 81

Population mean
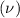`(\\u)` = 79

Standard deviation
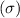`(\sigma )` = 18

​(a) Describe the sampling distribution of
`\overline{X}`

For large sample using central limit theorem

the sampling distribution of
`\overline{X}` = Population mean = 79

​(b) What is Upper P (
`\overline{X}` greater than 81.2 )​ =

`P(\overline{X}> 81.2)` =
`P(\frac{\overline{X} - \\u }{(\sigma )/(√(n))}> (81.2 - 79)/((18)/(√(81))))`

=
`P(Z> 1.1)`

=
`1 - P(Z< 1.1)`

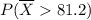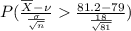
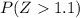
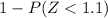
= 1 - .8643 =

= 0.1357

(c) What is Upper P (
`\overline{X}` less than or equals 74.4 ) =

`P(\overline{X}\leq 74.4)` =
`P(\frac{\overline{X} - \\u }{(\sigma )/(√(n))}\leq (74.4- 79)/((18)/(√(81))))`

=
`P(Z\leq -2.3)`

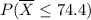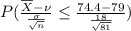
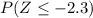
= .0107

​(d) What is Upper P (77.6 less than
`\overline{X}` less than 83.2 ) =

`P(77.6< \overline{X}< 83.2)` =
`P((77.6- 79)/((18)/(√(81))))< P(\frac{\overline{X} - \\u }{(\sigma )/(√(n))}\leq (83.2- 79)/((18)/(√(81))))`

=
`P(- 0.7< Z< 2.1)`

=
`(Z< 2.1) - (Z< -0.7)`

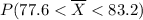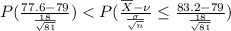
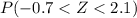
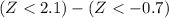
= 0.9821 - .2420

= 0.7401