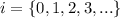Answer:
a)
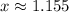 , b)
, b)
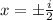 , for all
, for all
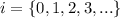
Explanation:
a) The slope associated with the mean value is:
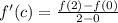
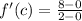
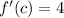
Let differentiate the function:
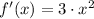
The value associated with the slope is:
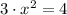
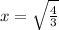
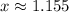
b) The slope associated with the mean value is:
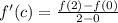
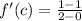
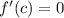
Let differentiate the function:
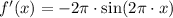
The value associated with the slope is:

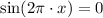
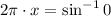
 , for all
, for all
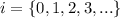
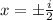 , for all
, for all