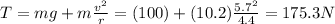Question

A heavy ball with a weight of 100 NN is hung from the ceiling of a lecture hall on a 4.4-mm-long rope. The ball is pulled to one side and released to swing as a pendulum, reaching a speed of 5.7 m/sm/s as it passes through the lowest point

Answer 1

175.3 N

Step-by-step explanation:

The motion of the ball is a uniform circular motion, therefore the net force on it must be equal to the centripetal force.

There are two forces acting on the ball at the lowest point of motion:

- The tension in the string, T , upward

- The weight of the ball,
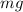`mg`, downward

The net force (centripetal force) has the same direction as the tension (upward, towards the centre of the circular path), so we can write:

`T-mg=m(v^2)/(r)`

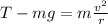
where the term on the right is the expression for the centripetal force, and where:

T is the tension in the string

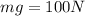`mg=100 N` is the weight of the ball

`m=(mg)/(g)=(100)/(9.8)=10.2 kg` is the mass of the ball

v = 5.7 m/s is the speed of the ball at the lowest point

r = 4.4 m is the length of the rope, so the radius of the circle

Solving for T, we find the tension in the string:

`T=mg+m(v^2)/(r)=(100)+(10.2)(5.7^2)/(4.4)=175.3 N`