Question

A ball is dropped from rest at a point 12 m above the ground into a smooth, frictionless chute. The ball exits the chute 2 m above the ground and at an angle 45o from the horizontal. Air resistance is negligible. Approximately how far will the ball travel in the horizontal direction before hitting the ground

Answer 1

x=1.78m

Step-by-step explanation:

To calculate the max distance it is necessary to fin the initial velocity of the ball when the ball leaves the chut. For that we have to know what is final speed in the first motion

By using the expression

`v^2=v_0^2+2gy\\\\v=\sqrt{2*9.8(m)/(s^2)(12m)}=15.33(m)/(s)`

the energy when the ball is at 2m must conserve, hence we have

`E_(ground)=E_(2m)\\\\(1)/(2)mv^2=(1)/(2)mv'^2+mgh\\\\v^2=v'^2+2gh\\\\v'=√(v^2-2gh)=\sqrt{(15.33(m)/(s))^2-2(9.8(m)/(s^2))(2m)}=13.99(m)/(s)`

13.99m\s is the initial velocity

The max distance of the ball is calculated by computing the time in wich the ball hit the ground

`y=y_0+v'sin\alpha t -(1)/(2)gt^2=0\\\\2+(13.99)sin(45\°)t-(1)/(2)(9.8)t^2=0\\\\2+9.89t-4.9t^2=0\\\\t=(-9.89+-√((9.89)^2+4(4.9)(2)))/(2(4.9))\\\\t_1=0.18s\\t_2=-15s\\`

we choose the positive value because it has physical meaning.

Finally:

`x_(max)=v'cos\alpha t=(13.99)cos(45\°)(0.18)=1.78m`

the xmax is approximately 1.78m

hope this helps!!

Answer 2

29,7 m

Step-by-step explanation:

We need to devide the problem in two parts:

A) Energy

B) MRUV

Energy:

Since no friction between pint (1) and (2), then the energy conservatets:

Energy = constant ----> Ek(cinética) + Ep(potencial) = constant

Ek1 + Ep1 = Ek2 + Ep2

Ek1 = 0 ; because V1 is zero (the ball is "dropped")

Ep1 = m*g*H1

Ep2= m*g*H2

Then:

Ek2 = m*g*(H1-H2)

By definition of cinetic energy:

m*(V2)²/2 = m*g*(H1-H2) --->
`V2 = √((2*g*(H1-H2))`

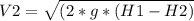
Replaced values: V2 = 14,0 m/s

MRUV:

The decomposition of the velocity (V2), gives a for the horizontal component:

V2x = V2*cos(α)

Then the traveled distance is:

X = V2*cos(α)*t.... but what time?

The time what takes the ball hit the ground.

Since: Y3 - Y2 = V2*t + (1/2)*(-g)*t²

In the vertical axis:

Y3 = 0 ; Y2 = H2 = 2 m

Reeplacing:

-2 = 14*t + (1/2)*(-9,81)*t²

solving the ecuation, the only positive solution is:

t = 2,99 sec ≈ 3 sec

Then, for the distance:

X = V2*cos(α)*t = (14 m/s)*(cos45°)*(3sec) ≈ 29,7 m