Question

Let f(x) be the probability density function for the lifetime of a manufacturer's highest quality car tire, where x is measured in miles. Explain the meaning of each integral. (a) 50,000 f(x) dx 40,000 The integral is the probability that a randomly chosen tire will have a lifetime under 50,000 miles. The integral is the probability that a randomly chosen tire will have a lifetime of exactly 50,000 miles. The integral is the probability that a randomly chosen tire will have a lifetime of at least 40,000 miles. The integral is the probability that a randomly chosen tire will have a lifetime between 40,000 and 50,000 miles.

Answer 1

(a) The integral in total indicates the probability of a randomly selected tire having a lifetime between 40,000 miles to 50,000 miles.

(b) The integral in total indicates the probability of a randomly selected tire having a lifetime of at least 25,000 miles.

Explanation:

The probability density function for the lifetime of a manufacturer's highest quality car tire is denoted by, f (x).

(a)

The integral given is:

`\int\limits^(50,000)_(40,000) {f(x)}\, dx`

The values 40,000 and 50,000 indicates the limits of the integral.

It implies that the integral is to be solved over the range (40,000 - 50,000) miles.

And the integral in total indicates the probability of a randomly selected tire having a lifetime between 40,000 miles to 50,000 miles.

(b)

The integral given is:

`\int\limits^(\infty)_(25,000) {f(x)}\, dx`

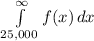
The values 25,000 and ∞ indicates the limits of the integral.

It implies that the integral is to be solved over the range (25,000 - ∞) miles.

And the integral in total indicates the probability of a randomly selected tire having a lifetime of at least 25,000 miles.