Question

A 4.0-m-diameter playground merry-go-round, with a moment of inertia of 350 kg⋅m2 is freely rotating with an angular velocity of 1.5 rad/s . Ryan, whose mass is 60 kg , runs on the ground around the outer edge of the merry-go-round in the opposite direction to its rotation. Still moving, he jumps directly onto the rim of the merry-go-round, bringing it (and himself) to a halt.How fast was Ryan running when he jumped on?

Answer 1

4.375 m/s

Step-by-step explanation:

Given that:

diameter of the playground merry-go-round = 4.0 m

then the radius will be = d/2 = 4/2 = 2.0 m

moment of Inertia (I) = 350 kg.m ²

angular velocity (ω) = 1.5 rad/s

mass (m) = 60 kg

Using conservation of angular momentum;

I ω = m V r

350 × 1.5 = 60 × V × 2

525 = 120 V

V =
`(525)/(120)`

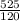
V = 4.375 m/s

Thus, Ryan was running 4.375 m/s when he jumped on

Answer 2

`v = 4.375\,(m)/(s)`

Step-by-step explanation:

The situation of the system Ryan - merry-go-round is modelled after the Principle of the Angular Momentum Conservation:

`(350\,kg\cdot m^(2))\cdot (1.5\,(rad)/(s) ) - (2\,m)\cdot (60\,kg)\cdot v = 0\,kg\cdot (m^(2))/(s)`

The initial speed of Ryan is:

`v = 4.375\,(m)/(s)`