Question

A 50-cm-long spring is suspended from the ceiling. A 330 g mass is connected to the end and held at rest with the spring unstretched. The mass is released and falls, stretching the spring by 20 cm before coming to rest at its lowest point. It then continues to oscillate vertically.a. What is the spring constant? (K=)

b. What is the amplitude of the oscillation?
c. What is the frequency of the oscillation?

Answer 1

a)32.34 N/m

b)10cm

c)1.6 Hz

Step-by-step explanation:

Let 'k' represent spring constant

'm' mass of the object= 330g =>0.33kg

a) in order to find spring constant 'k', we apply Newton's second law to the equilibrium position 10cm below the release point.

ΣF=kx-mg=0

k=mg / x

k= (0.33 x 9.8)/ 0.1

k= 32.34 N/m

b) The amplitude, A, is the distance from the equilibrium (or center) point of motion to either its lowest or highest point (end points). The amplitude, therefore, is half of the total distance covered by the oscillating object.

Therefore, amplitude of the oscillation is 10cm

c)frequency of the oscillation can be determined by,

f= 1/2π
`\sqrt{(k)/(m) }`

f= 1/2π
`\sqrt{(32.34)/(0.33) }`

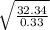
f= 1.57

f≈ 1.6 Hz

Therefore, the frequency of the oscillation is 1.6 Hz