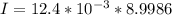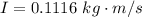Answer:
The impulse is
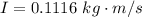
Step-by-step explanation:
Generally Impulse which the change in momentum is mathematically represented as
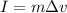
Where m is the mass with a value 12.4g =

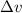 is the change in velocity which is mathematically represented as
is the change in velocity which is mathematically represented as
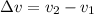
Where
 s the velocity of the marble drooping and
s the velocity of the marble drooping and
 is the velocity of the marble bouncing back
is the velocity of the marble bouncing back
setting up in a coordinate y-axis would show that
 is moving in the negative y-direction so the value would be
is moving in the negative y-direction so the value would be
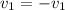 and
and
 is moving in the positive y-direction so the value would be
is moving in the positive y-direction so the value would be
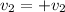
So the formula for
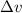 would be
would be
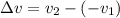
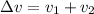
General v i mathematically represented as
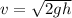
Substituting this into the formula for
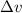
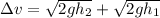
Now substituting values as given in the question
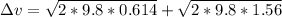
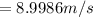
The impulse is