Answer:
8.75rad/s²
Step-by-step explanation:
The tires of the motorcycle undergo a rolling motion. Therefore, the tangential acceleration,
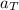 , of the tires is equal to their linear acceleration, a. i.e
, of the tires is equal to their linear acceleration, a. i.e
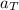 = a --------------(i)
= a --------------(i)
But, the tangential acceleration,
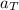 , is the product of the angular acceleration,
, is the product of the angular acceleration,
 , and the radius of the each of the tires. i.e
, and the radius of the each of the tires. i.e
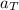 = r
= r
 ------------(ii)
------------(ii)
Combine equations (i) and (ii) as follows;
a = r
 --------------(iii)
--------------(iii)
Also, the linear acceleration, a, is given by;
a =
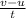 ------------------(iv)
------------------(iv)
Where;
v = final linear speed of the tire
u = initial linear speed of the tire
t = time taken for the motion
Combine equations iii and iv as follows;
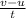 = r
= r
 ------------------(v)
------------------(v)
From the question;
v = 24.8m/s
u = 0 (since the motorcycle accelerates from rest)
t = 9.87s
r = 0.287m
Substitute these values into equation (v) as follows;
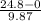 = 0.287
= 0.287

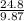 = 0.287
= 0.287

2.51 = 0.287

 =
=
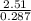
 = 8.75rad/s²
= 8.75rad/s²
Therefore, the angular acceleration of each tire is 8.75rad/s²