Question

A 16-year annuity pays $1,800 per month at the end of each month. If the discount rate is 8 percent compounded monthly for the first seven years and 10 percent compounded monthly thereafter, what is the present value of the annuity?

Answer 1

The present value of annuity is $657,720

Step-by-step explanation:

Present value of an annuity is the total cash value of all future annuity payments, given a determined rate of return or discount rate.

Present value of annuity = P
`[(1 - (1 + r)^(-n) )/(r)]`

where: P is the periodic payment, r is the rate per period and n is the number of periods.

The discount rate is compounded for the first 7 years and thereafter.

The present value of annuity in the first 7 years can be calculated as:

P = $1800 × 12 = $21,600 per year, r = 8% and n = 7 years.

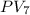`PV_(7)` = 21600
`[(1 - (1 + 0.08)^(-7) )/(0.08)]`

= 21600
`[(0.42)/(0.08)]`

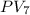`PV_(7)` = $113,400

Thus, the present value after the first 7 years = $113,400.

Therefore, the present value of the annuity = 113,400
`[(1 - (1 + 0.1)^(-9) )/(0.1)]`

= 113,400
`[(0.58)/(0.1)]`

= $657,720

The present value of annuity is $657,720.

Answer 2

PV = $188,653.22

Step-by-step explanation:

Given the following information, firstly we need to calculate present value of cash flow for the last 9 years. The present value of cash flow therefore

PVA2= $1,800 {[1 – 1 / (1 + 0.10 / 12)^108] / (0.10 / 12)}

PVA2= $127,852.84

Thus, present value of Cashflow today

PV = $127,852.84 / [1 + (0.08 / 12)]^84+ $1,800{[1 – 1 / (1 + 0.08 / 12)^84] / (0.08 / 12)}

PV = $188,653.22