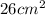Question

The circumference of a sphere was measured to be 82 cm with a possible error of 0.5 cm. (a) Use differentials to estimate the maximum error in the calculated surface area. (Round your answer to the nearest integer.) cm2

Answer 1

The Maximum error is
`26cm^2`

Explanation:

Given that the circumference of a sphere was measured to be 82 cm with a possible error of 0.5 cm

To find :

(a) Use differentials to estimate the maximum error in the calculated surface area. (Round your answer to the nearest integer.)
`cm^2`

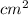
Given circumference of a sphere=82 cm and possible error =0.5 cm

Error of the surface area is dA

Error of circumference is dC = 0.5 cm

We know that the formula for Circumference of a sphere is C=2πr units

Differentiating with respect to r

`dC = 2\pi dr`

`dr =(dC)/(2π)`

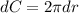
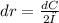
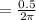`=(0.5)/(2\pi)` (∵ dC = 0.5 cm)

Since Area
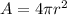`A = 4\pi r^2` square units

Differentiating with respect to r

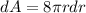`dA = 8\pi rdr` square units

Since given C = 82 cm.and also C=2πr we have

`r=(C)/(2π)`

`=(82)/(2π)`

`r=(41)/(π)`

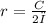
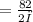
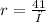
From that
`dA = 8\pi rdr`

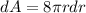
Substituting the values of r and dr in the above equation we get

`dA = 8\pi ((41)/(\pi)) ((0.5)/(2\pi))`

`=4(41)* ((0.5)/(3.14))`

`=26.1146`

`dA=26cm^2`

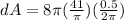
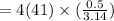
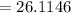
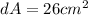
∴ Maximum error is
`26cm^2`