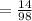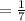Question

Forty of the marbles are red, 20 of the marbles are blue, 25 of the marbles are white, and 15 of the marbles are yellow. Assuming that you do NOT replace a marble after removing it from the jar, What is the probability that the first marble selected will be yellow? If the first marble selected was yellow, what is the probability that the second marble will be yellow? If the first two marbles selected were yellow, what is the probability that the third marble selected will be red?

Answer 1

The probability that the first selected marble will be yellow is
`\frac3{20}`.

The probability that the second selected marble will be yellow is
`(14)/(99)`.

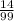The probability that the third selected marble will be red is
`\frac1 7`

Explanation:

Probability:

The ratio of the number of favorable outcomes to the the number of all possible outcomes.

Given that, in a jar, 40 of the marbles are red, 20 of marbles are blue, 25 of the marbles white and 15 of the marbles are yellow.

Total number of marbles is=(40+20+25+15)=100

The probability that the first selected marble will be yellow is

`=\frac{\textrm{Number of yellow marbles}}{\textrm{Total number of marbles}}`

`=(15)/(100)`

`=(3)/(20)`

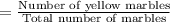
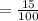
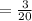
After first selected marble was yellow, the remains yellow marbles is

= (15-1)=14

Now total number of marble is =(100-1)=99

The probability that the second selected marble will be yellow is

`=\frac{\textrm{Number of yellow marbles}}{\textrm{Total number of marbles}}`

`=(14)/(99)`

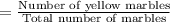
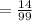
Now the total number of marble is =(99-1)=98

The probability that the third selected marble will be red is

`=\frac{\textrm{Number of red marbles}}{\textrm{Total number of marbles}}`

`=(14)/(98)`

`=\frac17`