Question

A social researcher claims that the average adult listens to the radio less than 26 hours per week. He collects data on 25 individuals' radio listening habits and finds that the mean number of hours that the 25 people spent listening to the radio was 22.4 hours. If the population standard deviation is known to be eight hours, can we conclude at the 1% significance level that he is right

Answer 1

There is not sufficient evidence to support the claim that average adult listens to the radio less than 26 hours per week at 0.01 significance level.

Explanation:

We are given the following in the question:

Population mean, μ = 26 hours per week

Sample mean,
`\bar{x}` = 22.4 hours per week

Sample size, n = 25

Alpha, α = 0.01

Population standard deviation, σ = 8 hours per week

First, we design the null and the alternate hypothesis

`H_(0): \mu = 26\text{ hours per week}\\H_A: \mu < 26\text{ hours per week}`

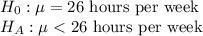
We use one-tailed z test to perform this hypothesis.

Formula:

`z_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

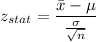
Putting all the values, we have

`z_(stat) = \displaystyle(22.4 - 26)/((8)/(√(25)) ) = -2.25`

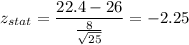
Now, we calculate the p-value from the table.

P-value = 0.0122

Since the p-value is greater than the significance level, we fail to reject the null hypothesis and accept it.

Conclusion:

Thus, there is not sufficient evidence to support the claim that average adult listens to the radio less than 26 hours per week at 0.01 significance level.