Answer:
(a) The distribution of X is N (100, 15²).
(b) The probability that a person has an IQ greater than 130 is 0.0228.
(c) The minimum IQ needed to qualify for the Mensa organization is 131.
(d) The middle 20% of IQs fall between 96 and 104.
Explanation:
The random variable X is defined as the IQ of an individual.
(a)
The random variable X is normally distributed with mean, μ = 100 and standard deviation, σ = 15.
The probability density function of X is:
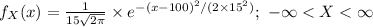
Thus, the distribution of X is N (100, 15²).
(b)
Compute the probability that a person has an IQ greater than 130 as follows:
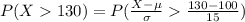
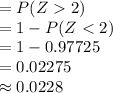
Thus, the probability that a person has an IQ greater than 130 is 0.0228.
(c)
Let x represents the top 2% of all IQs.
Then, P (X > x) = 0.02.
⇒ P (X < x) = 1 - 0.02
⇒ P (Z < z) = 0.98
The value of z is:
z = 2.06.
Compute the value of x as follows:
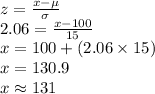
Thus, the minimum IQ needed to qualify for the Mensa organization is 131.
(d)
Let x₁ and x₂ be the values between which middle 20% of IQs fall.
This implies that:
![P(x_(1)<X<x_(2))=0.20\\P(-z<Z<z)=0.20\\P(Z<z)-P(Z<-z)=0.20\\P(Z<z)-[1-P(Z<z)]=0.20\\2P(Z<z)=1.20\\P(Z<z)=0.60](https://img.qammunity.org/2021/formulas/mathematics/college/ccf5otkh5ge6d8tr5at9y9sx0lb1jr6pis.png)
The value of z is:
z = 0.26.
Compute the value of x as follows:
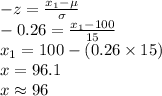
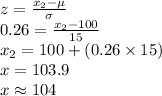
Thus, the middle 20% of IQs fall between 96 and 104.