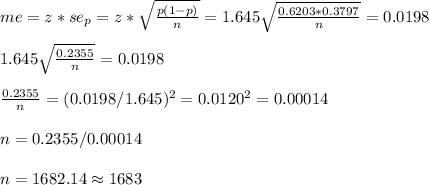Answer:
1) p-hat = 0.6203
2) std error = 0.0177
3) margin of error = 0.0291
4) (0.5912, 0.6494)
5) minimum sample size = 1683
Explanation:
1. The point estimate for the proportion of American adults that think licensed drivers should be required to retake their road test once they reach 65 years of age can be calculating dividing the number of people who answer Yes by the total of people interviewed:
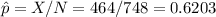
2. The standard error of a proportion can be expressed as:

3. The z-value for a 90% CI is z=1.64485.
The margin of error can be expressed as:
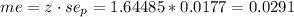
4. The lower and upper limits can be calculated as:
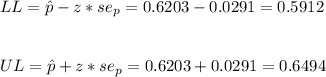
5. To have a margin of error of no more than 3.2% of the sample proportion, we have to first calculate what margin of error gives 3.2% of the proportion.
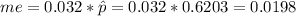
This margin of error can be related to the sample size as: