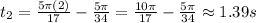Answer:
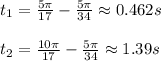
Step-by-step explanation:
No matter the coeficient of the cosine function, the function will always be zero as long as the following is true:
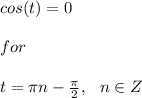
Now:
Rewrite 3.4 as:
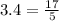
So:
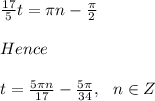
Therefore the particle crosses the x-axis (x(t)=0) :
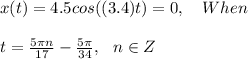
The first time is when n=1, so:
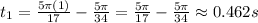
And the second time is when n=2, so: