Question

Suppose that a wall is constructed from concrete blocks where a block is a normal random variable with mean 11 kg and standard deviation 0.09 kg. If 85% of the blocks have weights less than k kg, evaluate k

Answer 1

The value for k is about k = 11.093kg.

Explanation:

To answer this question, that is, P(x<k) = 0.85, we can use the standardized value for a raw score, or the formula for obtaining z-scores:

`\\ z = (x - \mu)/(\sigma)` [1]

Where

`\\ x` is the raw score.

`\\ \mu` is the population mean.

`\\ \sigma` is the population standard deviation.

In this case, we are asking to find a value x = k, so that 85% of the blocks have weights less than k (kg).

We have also to use the values for the cumulative standard normal distribution with
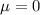`\\ \mu = 0` and
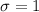`\\ \sigma = 1` to find the value of z that corresponds to a probability of 0.85.

First step: find the z that corresponds to the probability of 0.85.

To use the formula [1], as we previously mentioned, we first need to find the value of z that corresponds to a probability of 0.85 using the cumulative standard normal distribution table (available in any Statistics books or on the Internet). Then, for a cumulative probability of 0.85, the corresponding value for z = 1.03 (approximately).

Second step: solve the formula [1] for x.

Solving this formula for x, we have:

`\\ z = 1.03`

`\\ \mu = 11kg`

`\\ \sigma = 0.09kg`

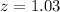
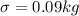
Then (without units):

`\\ z = (x - \mu)/(\sigma)`

`\\ 1.03 = (x - 11)/(0.09)`

`\\ 1.03*0.09 = x - 11`

`\\ (1.03*0.09) + 11 = x`

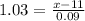
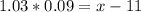
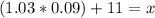
So

`\\ x = (1.03*0.09) + 11`

`\\ x = 0.0927 + 11`

`\\ x = 11.0927 \approx 11.093 = k`

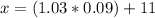
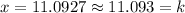
Thus, this value for x = 11.093 equals the value for k (x = k) so that

`\\ P(x<k) = 0.85`

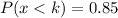
Then

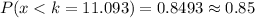`\\ P(x<k=11.093) = 0.8493 \approx 0.85` or

`\\ P(x<11.093) = 0.8493 \approx 0.85`

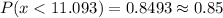
We can see the graph below showing this value of k = 11.093kg for which 85% of the blocks have weights less that it (x = k = 11.093kg).