Question

Maria looks at the equation (x - 5)(x - 6) = 2 and says that since the equation is in factored form it can be solved as follows: (x - 5)(x - 6) = 2 x - 5 = 2 and x - 6 = 2 x = 7 and x = 8 Explain to Maria why this is incorrect and explain to her the correct way to solve the equation

Answer 1

`x=7\text{ or }x=4`

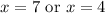
Explanation:

We have been given that Maria looks at the equation
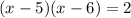`(x - 5)(x - 6) = 2` and says that since the equation is in factored form it can be solved as follows:

`x - 5=2\text{ and }x - 6= 2`

`x=7\text{ and }x=8`

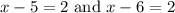
We are asked to explain why Maria's work is incorrect and what is the correct way to solve the equation.

We know that factored form of an equation is
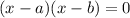`(x-a)(x-b)=0`. There should be 0 on right side of equation.

Since equation
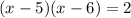`(x - 5)(x - 6) = 2` has 2 on right side, therefore, it is not is factored form.

First of all, we will expand left side of equation as:

`x(x-6)-5(x-6)= 2`

`x^2-6x-5x+30= 2`

`x^2-11x+30= 2`

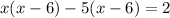
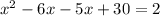
Upon subtracting 2 from both sides, we will get:

`x^2-11x+30-2= 2-2`

`x^2-11x+28=0`

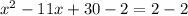
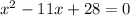
Upon splitting the middle term, we will get:

`x^2-7x-4x+28=0`

`x(x-7)-4(x-7)=0`

`(x-7)(x-4)=0`

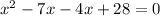
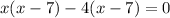
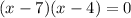
Using zero product property, we will get:

`x-7=0\text{ or }x-4=0`

`x=7\text{ or }x=4`

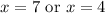
Therefore, the solutions for our given equation are
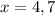`x=4,7`.