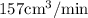Answer:
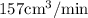
Explanation:
GIVEN: The height of a cylinder with a fixed radius of
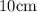 is increasing at the rate of
is increasing at the rate of
 .
.
TO FIND: rate of change of the volume of the cylinder (with respect to time) when the height is
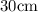 .
.
SOLUTION:
Let the height of cylinder be
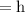
Let the volume of cylinder be
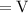
radius of cylinder is
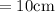
We know that
Volume of Cylinder
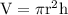
rate of change of height is

rate of change of volume is
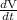
rate of change of volume when height is
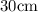

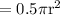
putting values

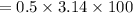

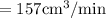
The rate of change of volume when height is
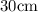 is
is