Question

rehistoric cave paintings were discovered in a cave in France. The paint contained 34 % of the original​ carbon-14. Use the exponential decay model for​ carbon-14, Upper A equals Upper A 0 e Superscript negative 0.000121 t​, to estimate the age of the paintings.

Answer 1

Therefore the age of paint is 8915.78 years.

Explanation:

Given that, the paint contain 34 % of the original carbon-14.

The exponential decay model for carbon-14 is

`A=A_0e^(-0.000121t)`

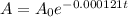
A= Remaining amount of carbon.

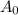`A_0` = initial amount of carbon.

Here A= 34% of
`A_0`
`=(34)/(100)A_0`

`\therefore (34)/(100)A_0=A_0e^(-0.000121t)`

`\Rightarrow (34)/(100)=e^(-0.000121t)`

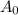
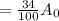
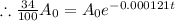
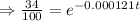
Taking ln both sides

`\Rightarrow ln|(34)/(100)|=ln|e^(-0.000121t)|`

`\Rightarrow ln|(34)/(100)|={-0.000121t`

`\Rightarrow t=(ln|(34)/(100)|)/(-0.000121)`

`\Rightarrow t= 8915.78`

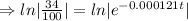
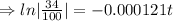
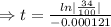
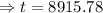
Therefore the age of paint is 8915.78 years.