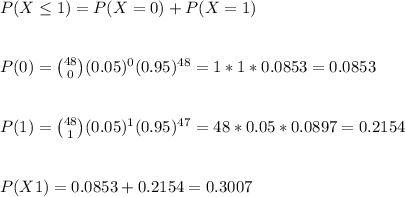Question

A pharmaceutical company receives large shipments of aspirin tablets. The acceptance sampling plan is to randomly select and test 4848 ​tablets, then accept the whole batch if there is only one or none that​ doesn't meet the required specifications. If one shipment of 30003000 aspirin tablets actually has a 55​% rate of​ defects, what is the probability that this whole shipment will be​ accepted? Will almost all such shipments be​ accepted, or will many be​ rejected?

Answer 1

a) The probability that this whole shipment will be​ accepted is 30%.

b) Many of the shipments with this rate of defective aspirin tablets will be rejected.

Explanation:

We have a shipment of 3000 aspirin tablets, with a 5% rate of defects.

We select a sample of size 48 and test for defectives.

If more than one aspirin is defective, the batch is rejected.

The amount of defective aspirin tablets X can be modeled as a binomial distribution random variable, with p=0.55 and n=48

We have to calculate the probabilities that X is equal or less than 1: P(X≤1).

`P(X\leq1)=P(X=0)+P(X=1)\\\\\\P(0)=\binom{48}{0}(0.05)^0(0.95)^(48)=1*1*0.0853=0.0853\\\\\\P(1)=\binom{48}{1}(0.05)^1(0.95)^(47)=48*0.05*0.0897=0.2154\\\\\\P(X\eq1)=0.0853+0.2154=0.3007`