Question

Simplify the expression by factoring, showing the steps in your work.

Answer 1

Given:

`$(12 x^(2)+31 x+7)/(16 x^(2)+8 x+1)`

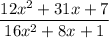
To find:

The simplified expression by factoring.

Solution:

Let us factor the numerator:

`12 x^(2)+31 x+7`

31x can be written as 3x + 28x.

`=\left(12 x^(2)+3 x\right)+(28 x+7)`

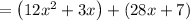
Take 3x common in 1st two terms and 7 common in next two terms.

`=3 x(4 x+1)+7(4 x+1)`

Make sure the remaining terms in the both brackets must be same.

Now, take out common factor (4x + 1).

`=(4 x+1)(3 x+7)`

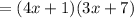
In the same way, factorize the denominator:

`16 x^(2)+8 x+1`

8x can be written as 4x + 4x.

`=(16 x^(2)+4 x)+(4x+1)`

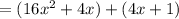
Take 4x common in 1st two terms and 1 common in next two terms.

`=4x(4 x+1)+1(4x+1)`

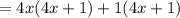
Make sure the remaining terms in the both brackets must be same.

Now, take out common factor (4x + 1).

`=(4x+1)(4x+1)`

Substitute the terms we found for numerator and denominator:

`$(12 x^(2)+31 x+7)/(16 x^(2)+8 x+1)=((4 x+1)(3 x+7))/((4 x+1)(4 x+1))`

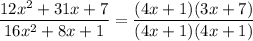
Cancel the common factors.

`$=(3 x+7)/(4 x+1)`

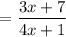
The simplified expression is
`(3 x+7)/(4 x+1)`.