Question

A fence must be built to enclose a rectangular area of 45 comma 000 ftsquared. Fencing material costs $ 3 per foot for the two sides facing north and south and ​$6 per foot for the other two sides. Find the cost of the least expensive fence.

Answer 1

150 feet by 300 feet.

Explanation:

The fence is to enclose a rectangular area of 45,000 ft squared.

If the dimensions of the rectangle are x and y

Area of a rectangle = xy

• xy=45000
• 
  `x=(45000)/(y)`

Perimeter of the Rectangle =2x+2y

Fencing material costs $ 3 per foot for the two sides facing north and south and ​$6 per foot for the other two sides.

• Cost of Fencing, C=$(6*2x+3*2y)=$(12x+6y)

Substitute
`x=(45000)/(y)` into the Cost to get C(y)

C=12x+6y

`C(y)=12((45000)/(y))+6y\\C(y)=(540000+6y^2)/(y)`

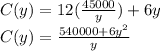
The value at which the cost is least expensive is at the minimum point of C(y), when the derivative is zero.

`C^(')(y)=(6y^2-540000)/(y^2)`

`(6y^2-540000)/(y^2)=0\\6y^2-540000=0\\6y^2=540000\\y^2=(540000)/(6) =90000\\y=√(90000)=300`

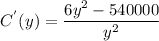
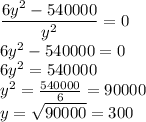
Recall,

`x=(45000)/(y)=(45000)/(300)=150`

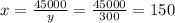
Since x=150, y=300

The dimensions that will be least expensive to build is 150 feet by 300 feet.