Question

The National Association of Realtors reported that 26% of home buyers in the state of Florida are foreigners. A random sample of 110 home buyers was selected and the number of foreigners was in the sample was 20. Test the validity of the report using the results of this sample at α=.10. Be sure to write your hypothesis testing statements, calculate the p-value, and draw a complete conclusion. 14 pts

Answer 1

Hypothesis

`H_0: \pi=0.26\\\\H_a: \pi\\eq 0.26`

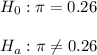
P-value = 0.078

Conclusion: The null hypothesis is rejected. There is enough evidence to claim that the proportion of foreigners home buyers is different from 26%.

Explanation:

We will perform a hypothesis test on a proportion.

The null hypothesis states that 26% of home buyers are foreigners.

The alternative hypothesis states that the proportion is different than 26%.

`H_0: \pi=0.26\\\\H_a: \pi\\eq 0.26`

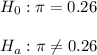
The significance level is α=0.10.

The sample proportion is:

`p=x/N=20/110=0.182`

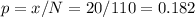
The standard error is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n) }=\sqrt{(0.26*0.74)/(110)} =\sqrt{(0.1924)/(110) } =√(0.00175) \\\\\sigma_p=0.042`

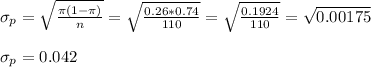
Then, we can calculate the z-statistic as:

`z=(p-\pi+0.5/N)/(\sigma_p) =(0.182-0.26+0.004)/(0.042)=- (0.074)/(0.042)= -1.762`

The P-value can be calculated as:

`P-value=2*P(z<-1.762)=0.078\\\\P-value<\alpha`

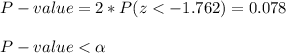
The P-value is smaller than the significance level, so the effect is significant.

The null hypothesis is rejected. There is enough evidence to claim that the proportion of foreigners home buyers is different from 26%.