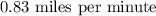Answer:
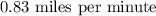
Explanation:
GIVEN: In a
 mile race, Janet covered the first
mile race, Janet covered the first
 miles at a constant rate. She then speed up and rode her bike the last
miles at a constant rate. She then speed up and rode her bike the last
 miles at a rate that was
miles at a rate that was
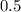 miles per minute faster. Janet's overall time would have been
miles per minute faster. Janet's overall time would have been
 minutes faster had she ridden her bike the whole race at the faster pace.
minutes faster had she ridden her bike the whole race at the faster pace.
TO FIND: What was Janet's average speed (in miles per minute) for the whole race?
SOLUTION:
let the speed of Janet in first
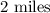
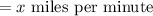
speed of Janet's bike in last
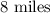
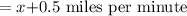
total time taken by Janet,
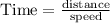

Time taken if Janet rides whole race at faster pace
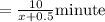
As, Janet's overall time would have been
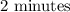 faster had she ridden her bike the whole race at the faster pace.
faster had she ridden her bike the whole race at the faster pace.
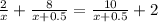
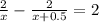
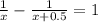
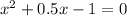
on solving we get
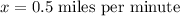

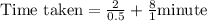

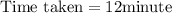
Average speed
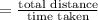
Average speed
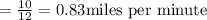
Therefore average speed of Janet was