Answer:
The temperature of star is 5473.87 K
Step-by-step explanation:
Given:
Energy difference
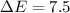 eV
eV
The ratio of number of particle
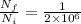
Degeneracy ratio
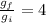
From the formula of boltzmann distribution for population levels,

Where
 boltzmann constant =
boltzmann constant =
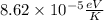
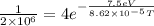
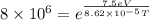
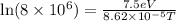

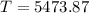 K
K
Therefore, the temperature of star is 5473.87 K