Answer:
A = 137° a = 14 cm
B = 26° b = 9 cm
C = 17° c = 6 cm
Explanation:
Cosine rule
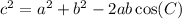
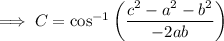
where:
- c is the side opposite angle C
- a and b are the sides with C as the included angle.
Given:
- a = 14 cm
- b = 9 cm
- c = 6 cm
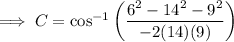
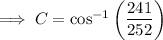
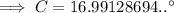
Sine Rule
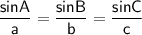
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
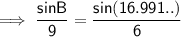
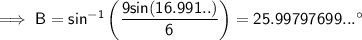
Sum of interior angles of a triangle = 180°
⇒ ∠A + ∠B + ∠C = 180°
⇒ ∠A = 180° - 25.997...° - 16.9912...°
⇒ ∠A = 137.0107361...°