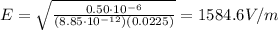Answer:
1584.6 V/m
Step-by-step explanation:
The energy density (the energy per unit volume) for an electromagnetic wave is given by the equation
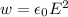
where
 is the vacuum permittivity
is the vacuum permittivity
E is the amplitude of the electric field of the wave
At the same time, the energy density can be written as
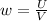
where
U is the total energy of the wave
V is the volume considered
So the first equation can be written as
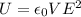
Or
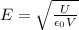
In this problem:
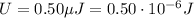 is the total energy of the microwave
is the total energy of the microwave
The volume considered is the volume of the cavity, so:
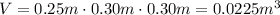
Therefore, the amplitude of the electric field is: