Question

The tallest free-standing tower in the world is the CN Tower in Toronto, Canada. The tower includes a rotating restaurant high above the ground. From a distance of 500 ft the angle of elevation to the pinnacle of the tower is LaTeX: 74.6^\circ74.6 ∘. The angle of elevation from the same vantage point on the ground to the restaurant is LaTeX: 66.5^\circ66.5 ∘. How tall is the CN Tower? How far below the pinnacle of the tower is the restaurant located? You need to discuss all the methods that you can use to the class how do you calculate the height of the tower and the distance from the rotating restaurant to the pinnacle.

Answer 1

(a)1815 feet

(b)665 feet

Explanation:

(a)From the diagram, we want to determine the height CN of the tower.

`Tan \theta =(Opposite)/(Adjacent) \\Tan 74.6 =(|CN|)/(500) \\|CN|=500 X Tan 74.6=1815.24 feet`

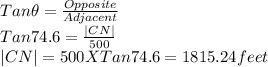
• The CN tower is 1815 feet tall.

(b)To determine how far below the pinnacle of the tower the restaurant is located. We are to determine the distance RN.

|CR|+|RN|=|CN|

First, we determine |CR|

`Tan \theta =(Opposite)/(Adjacent) \\Tan 66.5 =(|CR|)/(500) \\|CR|=500 X Tan 66.5=1149.92 feet`

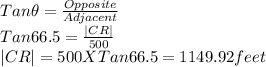
|CR|+|RN|=|CN|

|RN|=|CN|-|CR|=1815-1150=665 feet

The restaurant is located 665 feet below the pinnacle of the tower.