Question

The indicated function y1(x) is a solution of the given differential equation. Use reduction of order or formula (5) in Section 4.2, y2 = y1(x) e−∫P(x) dx y 2 1 (x) dx (5) as instructed, to find a second solution y2(x). y'' − 4y' + 4y = 0; y1 = e2x

Answer 1

`\therefore y_2(x)=-(e^(-6x))/(8)`

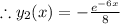
The general solution is

`y=c_1e^(2x)-c_2.(e^(-6x))/(8)`

Explanation:

Given differential equation is

y''-4y'+4y=0

and
`y_1(x)=e^(2x)`

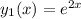
To find the
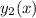`y_2(x)` we are applying the following formula,

`y_2(x)=y_1(x)\int (e^(-\int P(x) dx))/(y_1^2(x)) \ dx`

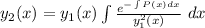
The general form of equation is

y''+P(x)y'+Q(x)y=0

Comparing the general form of the differential equation to the given differential equation,

So, P(x)= - 4

`\therefore y_2(x)=e^(2x)\int (e^(-\int 4dx))/((e^(2x))^2)dx`

`=e^(2x)\int (e^(-4x))/(e^(4x))dx`

`=e^(2x)\int e^(-4x-4x) \ dx`

`=e^(2x)\int e^(-8x) \ dx`

`=e^(2x). (e^(-8x))/(-8)`

`=-(e^(-6x))/(8)`

`\therefore y_2(x)=-(e^(-6x))/(8)`

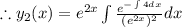
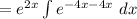
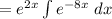
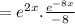
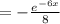
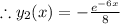
The general solution is

`y=c_1e^(2x)-c_2.(e^(-6x))/(8)`