Question

The triceps muscle in the back of the upper arm is primarily used to extend the forearm. Suppose this muscle in a professional boxer exerts a force of 2.25 × 103 N with an effective perpendicular lever arm of 2.75 cm, producing an angular acceleration of the forearm of 145 rad/s2. What is the moment of inertia of the boxer’s forearm?

Answer 1

To solve this problem we will apply the concepts related to Torque in its expression of both force and radius, as well as moment of inertia and acceleration. Next we will calculate the torque and then calculate the moment of inertia in the following way,

Torque generated due to this force is given as,

`\tau = Fr`

Here,

`\tau` = Torque

F = Force exerted

r = Radius of the lever arm

Replacing with our values

`\tau = (2.25*10^3N)(2.75*10^(-2)m)`

`\tau = 61.875N\cdot m`

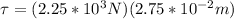
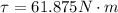
Moment of inertia of the boxer's forearm is given in relation to the angular acceleration and the torque, then

`\tau = I \alpha`

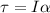
Here,

I = Moment of inertia

`\alpha` = Angular acceleration

Rearranging to find the Moment of inertia we have,

`I = (\tau)/(\alpha)`

`I = (61.875N\cdot m)/(145rad/s^2)`

`I = 0.426kg\cdot m^2`

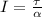
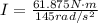
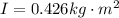
Therefore the moment of inertia of the boxer's forearm is
`0.426 kg \cdot m^2`