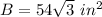Question

A design for party favors are in the shape of a regular hexagonal pyramid. The hexagon has a side length of 6 inches. The lateral faces are isosceles triangles with equal sides of 9 inches.

The lateral area of the pyramid is:
A) 1082
B) 903
C) 965

And the base area is:
A) 362
B) 543
C) 245

Answer 1

Part 1)
`LA=108√(2)\ in^2`

Part 2)
`B=54√(3)\ in^2`

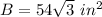
Explanation:

Part 1) Find the lateral area of the pyramid

we know that

The lateral area of the pyramid, is equal to the area of six congruent isosceles triangles

so

`LA=6[(1)/(2)(b)(h)]`

we have

`b=6\ in`

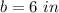
Applying Pythagorean Theorem calculate the height of triangle

`9^2=(6/2)^2+h^2`

`h^2=81-9\\h^2=72\\h=√(72)\ in`

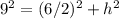
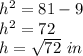
simplify

`h=6√(2)\ in`

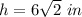
Find the lateral area

`LA=6[(1)/(2)(6)(6√(2))]\\\\LA=108√(2)\ in^2`

Part 2) Find the base area

we know that

The area of a regular hexagon is equal to the area of six equilateral triangles

so

Applying the law of sines to calculate the area of triangle

`B=6[(1)/(2)b^2sin(60^o)]`

we have

`b=6\ in`

`sin(60^o)=(√(3))/(2)`

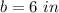
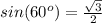
substitute

`B=6[(1)/(2)6^2((√(3))/(2))]`

`B=54√(3)\ in^2`