Question

In the game of​ roulette, a player can place a ​$8 bet on the number 17 and have a StartFraction 1 Over 38 EndFraction probability of winning. If the metal ball lands on 17​, the player gets to keep the ​$8 paid to play the game and the player is awarded an additional ​$280. ​ Otherwise, the player is awarded nothing and the casino takes the​ player's ​$8. What is the expected value of the game to the​ player? If you played the game 1000​ times, how much would you expect to​ lose?

Answer 1

Expected value of the game: -$0.421

Expected loss in 1000 games: $421

Explanation:

There are two possible outcomes for the event:

- There is a 1 in 38 chance of winning $280

- There is a 37 in 38 chance of losing $8

The expected value for a single game is:

`E(X) = (1)/(38)*\$280-(37)/(38)*\$8\\E(X)=-\$0.421`

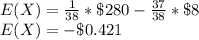
The expected value of the game is -$0.421

In 1,000 plays, the expected loss is:

`L = 1,000*-\$0.421\\L=-\$421`

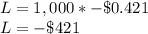
You would expect to lose $421.