Answer:
The sample size required is 22.
Explanation:
The random variable X can be defined as the scale readings of a lab scale.
The random variable X is normally distributed with standard deviation, σ = 0.0002 grams.
The procedure is repeated five times, i.e. the sample size is, n = 5.
The sample mean reading is,
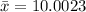 .
.
The (1 - α)% confidence interval for the population mean is:
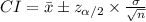
The margin of error of this interval is:
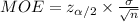
The critical value of z for 98% confidence interval is:

*Use a z-table.
Compute the sample size required to get a margin of error of 0.0001 as follows:
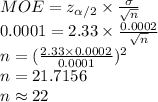
Thus, the sample size required is 22.