Question

To assess the accuracy of a lab scale, a standard weight known to weigh 10 grams is weighed repeatedly. The scale readings are normally distributed with unknown mean and the standard deviation of the scale reading is known to be 0.0002 grams. The following procedure could be used to test whether the scale is accurate (i.e., does the reported weight from the scale equal 10 gramsa. The weight is measured 5 times. The mean result is 10.0023 grams. Give a 98% confidence interval for the mean of repeated measurements of the weight.b. How many measurements must be averaged to get a margin of error of ±0.0001 with 98% confidence?

Answer 1

The sample size required is 22.

Explanation:

The random variable X can be defined as the scale readings of a lab scale.

The random variable X is normally distributed with standard deviation, σ = 0.0002 grams.

The procedure is repeated five times, i.e. the sample size is, n = 5.

The sample mean reading is,
`\bar x=10.0023`.

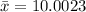The (1 - α)% confidence interval for the population mean is:

`CI=\bar x\pm z_(\alpha/2)* (\sigma)/(√(n))`

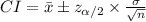
The margin of error of this interval is:

`MOE=z_(\alpha/2)* (\sigma)/(√(n))`

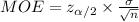
The critical value of z for 98% confidence interval is:

`z_(\alpha/2)=z_(0.02/2)=z_(0.01)=2.33`

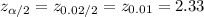
*Use a z-table.

Compute the sample size required to get a margin of error of 0.0001 as follows:

`MOE=z_(\alpha/2)* (\sigma)/(√(n))\\0.0001=2.33* (0.0002)/(√(n))\\n=((2.33* 0.0002)/(0.0001))^(2)\\n=21.7156\\n\approx22`

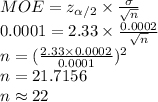
Thus, the sample size required is 22.