Answer:
The rotational kinetic energy is 19271.07 Joules.
Step-by-step explanation:
Given that,
Mass of the motorcycle, m = 14 kg
Angular velocity of the wheel,
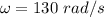
Inner radius is 0.270 m,
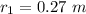
Outer radius,
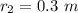
The rotational kinetic energy of the wheel is given by :
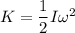
I is moment of inertia of the wheel,
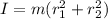
So,
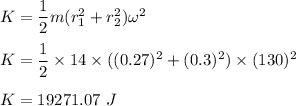
So, the rotational kinetic energy is 19271.07 Joules.