Answer:
(a)2000 of cells were present initially.
(b)The differential equation of the given exponential model is
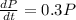
(c)The population will be double after 2.31 hours.
(d)The number of cell will be 8,000 after 4.62 hours.
Explanation:
Given that,
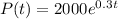
where P(t) is number of cell and t is time in hours.
(a)
Initial time means t=0.
Putting t=0 i the given expression
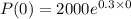

2000 of cells were present initially.
(b)
The differential equation of population growth is
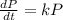
The solution of the above equation is
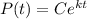
Comparing the given exponential model to the above solution
So, k= 0.3 and C=2000
The differential equation of the given exponential model is
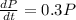
(c)
If the population double then P(t) = 2× P(0) =2×2000
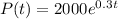
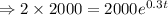
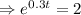
Taking ln both sides
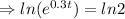
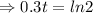
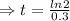
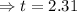 h
h
The population will be double after 2.31 hours.
(d)
Now P(t)=8,000
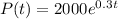
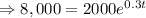
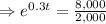
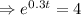
Taking ln function both sides
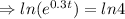
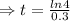
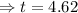 h
h
The number of cell will be 8,000 after 4.62 hours.