Answer:
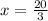 units and
units and
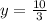 units is required to maximize the weight.
units is required to maximize the weight.
Explanation:
Given weight function is,

where x and y are number of units of first and second ingredients respectively.
To find how many units of each ingredient will maximize the weight we have to find the maximum value of weight function.
- First we have to find the critical points, differentiate partially (1) with respect to x and make it eual to zero we get,
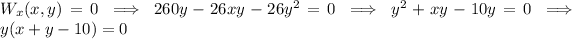
 Either, y=0 or,
Either, y=0 or,

And, differentiate partially (1) with respect to y and make it equal to zero we get,
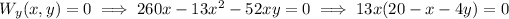
 Either, x=0 or,
Either, x=0 or,

Solving (2) and (3) we will get,
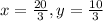 .
.
Hence critical points of (1) are (0,0) and
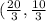
- Now to find maxima we have to verify both points.
Consider,
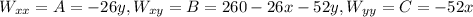
So that,
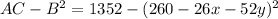
At (0,0),
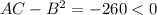
that is (0,0) is a local minima.
At
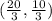
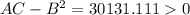
Which imply
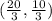 is local maxima of (1).
is local maxima of (1).
Therefore
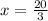 unit and
unit and
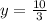 unit is required to maximize the weight.
unit is required to maximize the weight.