Question

Unpolarized light passes through a vertical polarizing filter, emerging with an intensity I0. The light then passes through a horizontal filter, which blocks all of the light; the intensity transmitted through the pair of filters is zero. Suppose a third polarizer with axis 45 ∘ from vertical is inserted between the first two. What is the transmitted intensity now?

Answer 1

To solve this problem it is necessary to apply the concepts related to Malus' law. Malus' law indicates that the intensity of a linearly polarized ray of light that passes through a perfect analyzer with a vertical optical axis is equivalent to:

`I = I_0 cos^2(\theta)`

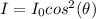
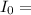`I_0 =` Indicates the intensity of the light before passing through the Polarizer,

I = The resulting intensity, and

`\theta` = Indicates the angle between the axis of the analyzer and the polarization axis of the incident light.

There is 3 polarizer, then

For the exit of the first polarizer we have that the intensity is,

`I_2 = I_0cos^2(45)`

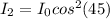
For the third polarizer then we have,

`I_3 = I_2 cos^(2)(45)`

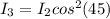
Replacing with the first equation,

`I_3 = I_0cos^2(45)cos^(2)(45)`

`I_3 = I_0 ((1)/(2))((1)/(2))`

`I_3 = I_0 (1)/(4)`

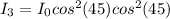
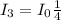
Therefore the transmitted intensity now is
`(1)/(4)` of the initial intensity.