Question

5. Projectile A with mass m is launched at an angle of 20° above the horizontal with a speed v0. Projectile B also with mass m is launched from the same location at an angle of 70° above the horizontal, also with speed v0. Thus, both projectiles have the same initial total energy. a. Which projectile has a larger speed when it hits the ground or do they have the same speed? Explain using energy. b. Which projectile reaches a greater height? Given that both projectiles have the same initial energy, how is this possible?

Answer 1

a) They both have the same final speed.

b) Projectile B reaches a greater height

Step-by-step explanation:

The initial total energy of both projectiles is the same, and since the initial height is zero, that initial energy is entirely kinetic energy:

`E_0=K_0=(1)/(2)mv_0^(2)`

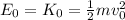
Now, when the projectiles are going to reach the ground, their height also becomes zero, so the final energy is also entirely kinetic energy:

`E_f=K_f=(1)/(2)mv_f^(2)`

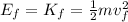
As stated in the conservation of mechanical energy, the final total energy has to be equal to the initial total energy, and then:

`E_0=E_f\\ \\ (1)/(2)mv_0^(2)=(1)/(2)mv_f^(2)\\\\\implies v_0=v_f`

Finally, since the initial speed is the same for both projectiles, they have the same speed when they hit the ground (a).

Next, we know that the height reached by a projectile depends only of their initial vertical velocity, nor their horizontal one. So, the projectile with the highest initial vertical velocity has to reach a greater height. We use trigonometry to calculate that:

`v_0_A_y=v_0\sin20\°=0.34v_0\\\\v_0_B_y=v_0\sin70\°=0.93v_0`

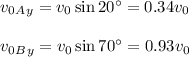
It means that projectile B has a higher initial vertical velocity, so it reaches a greater height (b).

This is possible because some of the kinetic energy of both projectiles is never transformed to gravitational potential energy (because is related to the horizontal velocity) and this amount of kinetic energy depends on the angle at which the projectile is launched. As their potential energies at the highest points are different, their maximum heights are, too.