Question

A ball with a mass of 3.1 kg is moving in a uniform circular motion upon a horizontal surface. The ball is attached at the center to a nail with a 2.0-m long rope and the tension in the rope is 20.4 N. Assuming no friction is taking place, how long does it take for the mass to make one complete revolution

Answer 1

3.46 seconds

Step-by-step explanation:

Since the ball is moving in circular motion thus centripetal force will be acting there along the rope.

The equation for the centripetal force is as follows -

`F=(mv^2)/(r)`

Where,
`m` is the mass of the ball,
`v` is the speed and
`r` is the radius of the circular path which will be equal to the length of the rope.

This centripetal force will be equal to the tension in the string and thus we can write,

`20.4 = (3.1* v^2)/(2)`

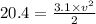
and,
`v^2 = 13.16`

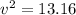
Thus,
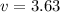`v = 3.63` m/s.

Now, the total length of circular path = circumference of the circle

Thus, total path length = 2πr = 2 × 3.14 × 2 = 12.56 m

Time taken to complete one revolution =
`\frac{\text {Path length} }{\text {Speed}}` =
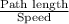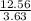`(12.56)/(3.63)` = 3.46 seconds.

Thus, the mass will complete one revolution in 3.46 seconds.