Question

What is the midline equation of the function g(x)=3\sin(2x-1)+4g(x)=3sin(2x−1)+4g, (, x, ), equals, 3, sine, (, 2, x, minus, 1, ), plus, 4?

Answer 1

Required equation of midline is x=4.

Explanation:

Given function is,

`g(x)=3\sin (2x-1)+4\hfill (1)`

In standerd form (1) can be written as,

`a\sin (bx+c)\pm d`

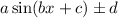
where,

|a|= amplitude.

b= vertical shift.

c= horizontal shift.

Midline is the line which runs between maximum and minimum value.

In this problem,

a=3, b=2, c=-1, d=4

So amplitude a=3 and graph is shifted 4 units in positive y-axis.

Therefore,

Maximum value = d + a = 4 + 3 = 7

Minumum value = d - a = 4 - 3 = 1

Midline will be centered of the region (7, 1) that is at 4.

Hence equation of midline is x=4.