Answer:
the initial deficit of oxygen of the mixture just downstream of the discharge point = 2.44 mg/L
Step-by-step explanation:
From the diagram ; we determine the dissolved oxygen just downstream by using the equation

where;
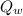 = volumetric flow rate of waste water = 1 m³/s
= volumetric flow rate of waste water = 1 m³/s
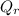 = volumetric flow rate of river just upstream of discharge point = 10 m³/s
= volumetric flow rate of river just upstream of discharge point = 10 m³/s
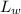 = ultimate BOD of waste water = 4 mg/L
= ultimate BOD of waste water = 4 mg/L
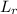 = ultimate BOD of mixture of the stream water and waste water = 8 mg/L
= ultimate BOD of mixture of the stream water and waste water = 8 mg/L
∴ DO =
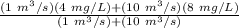
DO = 7.64 mg/L
Now; to calculate the initial deficit of oxygen; we use the formuale
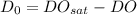
where;
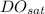 = the saturated value of the dissolved oxygen
= the saturated value of the dissolved oxygen
since no presence of chloride in the stream; chloride concentration = 0 mg/L
However, we obtain the saturated dissolved oxygen from Table - 5.10 " Solubility of oxygen in water at 1 atm corresponding to the temperature at 15° C and 0 mg/L concentration of chloride = 10.08 mg/L
SO,
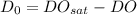

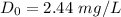
Thus; the initial deficit of oxygen of the mixture just downstream of the discharge point = 2.44 mg/L