Answer:
The minimum thickness of the oil is 77.55 nm
Step-by-step explanation:
Given:
Refractive index of oil

Refractive index of water
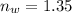
Wavelength of light
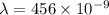 m
m
From the equation of thin film interference,
The minimum thickness is given by,
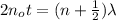
Where
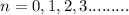 ,
,
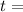 thickness
thickness
Here we have to find minimum thickness so we use
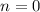
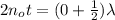
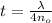
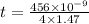
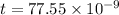 m
m
 nm
nm
Therefore, the minimum thickness of the oil is 77.55 nm