Question

A professor thinks that the students in her statistics class this term are less creative than most students at this university. A previous study found that students at this university had a mean score of 35 on a standard creativity test and scores were normally distributed. The professor finds that her class of 23 students scores a mean of 33 on this scale, with a standard deviation of 5. Using a .01 significance level, what is the correct decision and conclusion

Answer 1

It is not enough evidence to reject null hypothesis. It is not enough evidence to say that mean score is not equal to 35.

Explanation:

`\mu=35\\n=23\\\=x=33\\s=5\\\alpha=0.1`

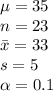
1. Null and alternative hypothesis

`H_(0):\mu=35\\H_(1):\mu<35`

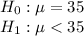
2. Significance level

`\alpha=0.1\\1-\alpha=0.99`

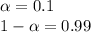
Freedom degrees is given by:

`v=n-1\\v=23-1=22`

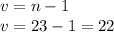
For a sgnificance level of 0,01 and 22 freedom degrees, t-student distribution value is:

`t_(0.01;23)=-2. 5083`

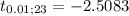
3. Test statistic

`t=(\=x-\mu)/((s)/(√(n) ) )`

`t=(33-35)/((5)/(√(23) ) )`

`t=-1,918`

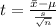
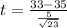
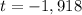
In this case, we have an one left tailed analysis, it means that null hypothesis is rejected if
`t<t_(\alpha;n-1)`

`-1.918>-2.5083`

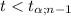
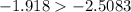
Conclusion:

It is not enough evidence to reject null hypothesis. It is not enough evidence to say that mean score is not equal to 35.