Question

When the current in a toroidal solenoid is changing at a rate of 0.0290 A/s, the magnitude of the induced emf is 12.3 mV. When the current equals 1.40 A, the average flux through each turn of the solenoid is 0.00251 Wb.How many turns does the solenoid have?

Answer 1

The solenoid has 237 turns.

Step-by-step explanation:

Given that, the current in a solenoid is changing at a rate
`(di)/(dt)=0.0290 \ A/s`

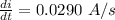
The magnitude of induced emf is
`\varepsilon` = 12.3 mV=
`12.3 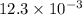* 10^(-3)` v when the current flows i=1.40 A.

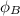`\phi_B`= 0.00251 is the magnitude of magnetic flux through each turns.

We need to find out the number of turns (N).

The induced emf of a solenoid is

`\varepsilon =L|(di)/(dt)|`

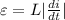
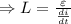`\Rightarrow L=(\varepsilon)/((di)/(dt))` ....(1)

The self inductance of solenoid is

`L=(N\phi_B)/(i)` ......(2)

From (1) and (2) we get

`(N\phi_B)/(i)=(\varepsilon)/((di)/(dt))`

`\Rightarrow (N* 0.00251)/(1.40)=(12.3* 10^(-3))/(0.0290)`

`\Rightarrow N=(12.3* 10^(-3)* 1.40)/(0.0290* 0.00251)`

`\Rightarrow N\approx 237`

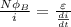
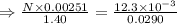
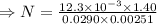
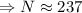
The solenoid has 237 turns.