Answer:
Yes, H is a subspace
Explanation:
Recall that given a vector space V, a subset W of V is a subspace if and only if
- the 0 of V is in W
- given a, b in W, then a+b is in W
- given a real scalar r and a in W, then ra is in W.
In order to see if H is a subspace of
 we must check the three properties.
we must check the three properties.
- It is clear that the matrix 0 in
 is in H since
is in H since
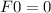 (where the right hand 0 is the 0 vector in
(where the right hand 0 is the 0 vector in
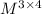 .
.
- Let A,B in H. We want to check that A+B is in H. Since A,B in H we have that FA=0 and FB=0. We have that
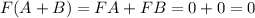
Then A+B is in H.
- given a real number r, and a matrix A in H, we want to check if rA is in H. Then

which shows that rA is in H.
Hence, H is a subspace of
